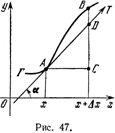
Пусть функция y=f(x) дифференцируема в точке х: т.е. для её приращения Dу в этой точке выполняется равенство [2]. Тогда Dу есть сумма двух слагаемых. Первое из них A Dx пропорционально Dx, а в таких случаях говорят, что оно есть линейная однородная функция от Dх. Второе – о(Dх)Dx®0 является бесконечно малой функцией высшего порядка малости сравнительно с Dx. Если А¹0, то второе слагаемое стремится к нулю при Dx®0 быстрее, чем первое. В связи с этим первое слагаемое A Dx=f'(x)Dx наз. главным членом приращения Dy. Это слагаемое называют дифференциалом функции и обозначают символом dy. Итак, по определению dy=df=f'(x)Dx. На (рис. 47) изображен график Г функции y=f(x); Т –касательная к Г в точке A, имеющей абсциссу х; f'(x)=tga, где a – угол, образованный касательной с осью х; dy=f'(х)Dx=tgaDx=CD, DB=Dy–dy=o(Dx)Dx®0. Таким образом, дифференциал функции у в точке х, соответствующий приращению Dx, есть приращение ординаты точки, лежащей на касательной (dy=CD). Вообще говоря, dy¹Dy, ибо Dy=dy+o(Dx)Dx®0, а второй член этой суммы, вообще говоря, не равен нулю. Только для линейной функции у=Ах+В имеет место равенство Dу=А Dx=dy для любого х. В частности, для у=х, dy=dx=Dx т.е. дифференциал и приращение независимой переменной равны между собой (dx=Dx). Поэтому дифференциал произвольной функции f обычно записывают так: dy=f'(x)dx, откуда f'(x)=dy/dx,
т.е. производная функции f в точке х равна отношению дифференциала функции в этой точке к дифференциалу независимой переменной х.
Это объясняет, что выражение dy/dx употребляется как символ для обозначения производной. Надо иметь в виду, что дифференциал dx независимой переменной не зависит от х, он равен Dx – произвольному приращению аргумента х. Что же касается дифференциала dy функции у (отличной от х), то он зависит от х и dx. Отметим формулы:
d(u±u¹)=du±du [3]; d(u×u)=udu+udu [4]; d(cu)=cdu (c – постоянная) [5]; d(u/u)=(udu–udu)/u2 (при u¹0) [6]; где предполагается, что u и u – дифференцируемые функции в рассматриваемой точке х. Например, формула [6] доказывается так:
