4Первый замечательный предел равен 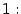
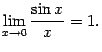
Доказательство. Рассмотрим два односторонних предела 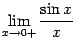 и
и 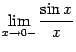 и докажем, что каждый из них равен 1. Тогда по теореме 2.1 двусторонний предел
и докажем, что каждый из них равен 1. Тогда по теореме 2.1 двусторонний предел 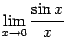 также будет равняться 1.
также будет равняться 1.
Итак, пусть 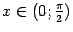 (этот интервал -- одно из окончаний базы
(этот интервал -- одно из окончаний базы 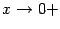 ). В тригонометрическом круге (радиуса
). В тригонометрическом круге (радиуса 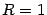 ) с центром
) с центром 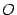 построим центральный угол, равный
построим центральный угол, равный 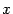 , и проведём вертикальную касательную в точке
, и проведём вертикальную касательную в точке 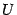 пересечения горизонтальной оси с окружностью (
пересечения горизонтальной оси с окружностью (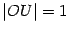 ). Обозначим точку пересечения луча с углом наклона
). Обозначим точку пересечения луча с углом наклона 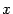 с окружностью буквой
с окружностью буквой 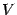 , а с вертикальной касательной -- буквой
, а с вертикальной касательной -- буквой 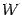 ; через
; через 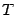 обозначим проекцию точки
обозначим проекцию точки 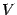 на горизонтальную ось.
на горизонтальную ось.
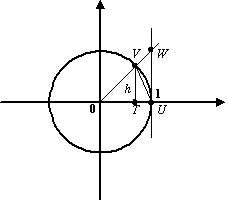
Пусть 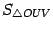 -- площадь треугольника
-- площадь треугольника 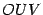 ,
, 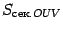 -- площадь кругового сектора
-- площадь кругового сектора 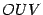 , а
, а 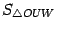 -- площадь треугольника
-- площадь треугольника 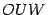 . Тогда очевидно следующее неравенство:
. Тогда очевидно следующее неравенство:
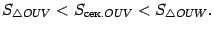
Заметим, что горизонтальная координата точки 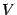 равна
равна 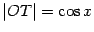 , а вертикальная --
, а вертикальная -- 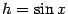 (это высота треугольника
(это высота треугольника 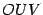 ), так что
), так что 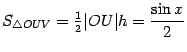 . Площадь центрального сектора круга радиуса
. Площадь центрального сектора круга радиуса 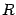 с центральным углом
с центральным углом 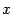 равна
равна 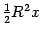 , так что
, так что 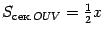 . Из треугольника
. Из треугольника 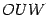 находим, что
находим, что 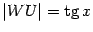 . Поэтому
. Поэтому 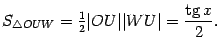 Неравенство, связывающее площади трёх фигур, можно теперь записать в виде
Неравенство, связывающее площади трёх фигур, можно теперь записать в виде
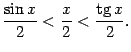
Все три части этого неравенства положительны, поэтому его можно записать так:
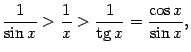
или (умножив на 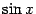 ) так:
) так:
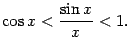
Предел постоянной 1 в правой части неравенства, очевидно, равен 1. Если мы покажем, что при 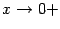 предел
предел 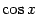 в левой части неравенства тоже равен 1, то по теореме "о двух милиционерах" предел средней части
в левой части неравенства тоже равен 1, то по теореме "о двух милиционерах" предел средней части 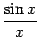 также будет равен 1.
также будет равен 1.
Итак, осталось доказать, что 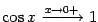 . Сперва заметим, что
. Сперва заметим, что 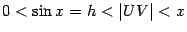 , так как
, так как 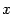 равняется длине дуги окружности
равняется длине дуги окружности 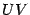 , которая, очевидно, длиннее хорды
, которая, очевидно, длиннее хорды 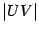 . Применяя теорему "о двух милиционерах" к неравенству
. Применяя теорему "о двух милиционерах" к неравенству
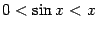
при 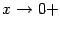 , получаем, что
, получаем, что
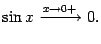 |
(2.3) |
Простая замена переменной 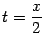 показывает, что и
показывает, что и 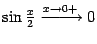 . Теперь заметим, что
. Теперь заметим, что 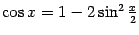 . Применяя теоремы о линейности предела и о пределе произведения, получаем:
. Применяя теоремы о линейности предела и о пределе произведения, получаем:
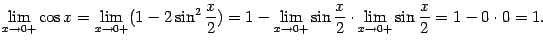 |
(2.4) |
Тем самым показано, что
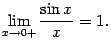
Сделаем теперь замену 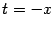 ; при этом база
; при этом база 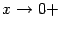 перейдёт в базу
перейдёт в базу 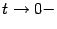 (что означает, что если
(что означает, что если 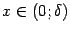 , то
, то 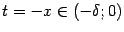 ). Значит,
). Значит,
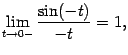
но 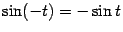 (
(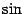 -- нечётная функция), и поэтому
-- нечётная функция), и поэтому 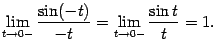 Мы показали, что левосторонний предел также равен 1, что и завершает доказательство теоремы
Мы показали, что левосторонний предел также равен 1, что и завершает доказательство теоремы
В9.Второй замечательный предел
Теорема lim(1+1/x)x=e
x®+¥
Доказательство:Пусть n – целая часть х – n=[x] n£x<n+1
[1+1/(n+1)]n£(1+1/x)x£(1+1/n)n+1
Если x®+¥, то n®+¥
[1+1/(n+1)]n+11/[1+1/(n+1)]£(1+1/x)x£(1+1/n)n(1+1/n) Þ lim(1+1/x)x=e
x®+¥
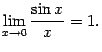
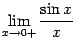 и
и 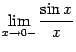 и докажем, что каждый из них равен 1. Тогда по теореме 2.1 двусторонний предел
и докажем, что каждый из них равен 1. Тогда по теореме 2.1 двусторонний предел 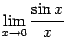 также будет равняться 1.
также будет равняться 1. 
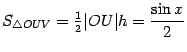 . Площадь центрального сектора круга радиуса
. Площадь центрального сектора круга радиуса 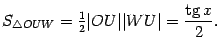 Неравенство, связывающее площади трёх фигур, можно теперь записать в виде
Неравенство, связывающее площади трёх фигур, можно теперь записать в виде 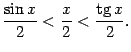
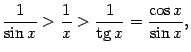
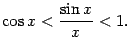
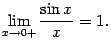
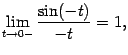
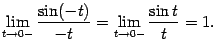 Мы показали, что левосторонний предел также равен 1, что и завершает доказательство теоремы
Мы показали, что левосторонний предел также равен 1, что и завершает доказательство теоремы